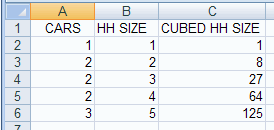
• Multiple regression using the Data Analysis Add-in.
• Interpreting the regression statistic.
• Interpreting the ANOVA table (often this is skipped).
• Interpreting the regression coefficients table.
• Confidence intervals for the slope parameters.
• Testing for statistical significance of coefficients
• Testing hypothesis on a slope parameter.
• Testing overall significance of the regressors.
• Predicting y given values of regressors.
• Excel limitations.

MULTIPLE REGRESSION USING THE DATA ANALYSIS ADD-IN

We then create a new variable in cells C2:C6, cubed household size as a regressor.
Then in cell C1 give the the heading CUBED HH SIZE.
(It turns out that for the se data squared HH SIZE has a coefficient of exactly 0.0 the cube is used).

The spreadsheet cells A1:C6 should look like:

We have regression with an intercept and the regressors HH SIZE and CUBED HH SIZE

The population regression model is:    y = β₁ + β₂ x₂ + β₃  x₃ + u
It is assumed that the error u is independent with constant variance (homoskedastic) - see EXCEL LIMITATIONS at the bottom.

We wish to estimate the regression line:     y = b₁ + b₂ x₂ + b₃ x₃

We do this using the Data analysis Add-in and Regression.

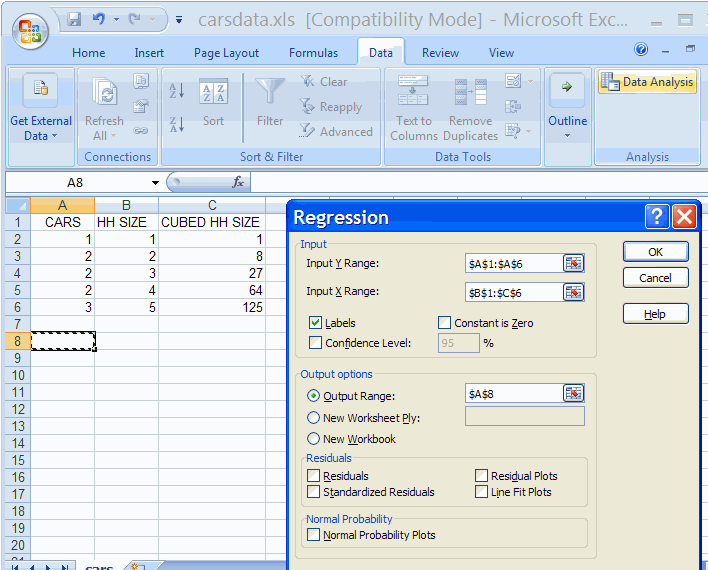
The only change over one-variable regression is to include more than one column in the Input X Range.
Note, however, that the regressors need to be in contiguous columns (here columns B and C).
If this is not the case in the original data, then columns need to be copied to get the regressors in contiguous columns.

Hitting OK we obtain

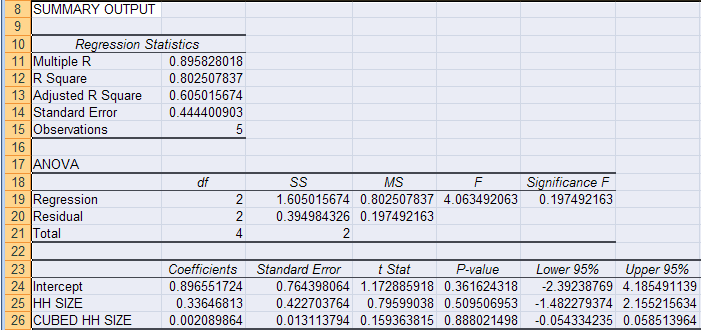
The regression output has three components:

• Regression statistics table
• ANOVA table
• Regression coefficients table.

This is the following output. Of greatest interest is R Square.
 

		Explanation
Multiple R	0.895828	R = square root of R2
R Square	0.802508	R2
Adjusted R Square	0.605016	Adjusted R2 used if more than one x variable
Standard Error	0.444401	This is the sample estimate of the standard deviation of the error u
Observations	5	Number of observations used in the regression (n)

The above gives the overall goodness-of-fit measures:
      R² = 0.8025
      Correlation between y and y-hat is 0.8958 (when squared gives 0.8025).
      Adjusted R² = R² - (1-R² )*(k-1)/(n-k) = .8025 - .1975*2/2 = 0.6050.

The standard error here refers to the estimated standard deviation of the error term u.
It is sometimes called the standard error of the regression. It equals sqrt(SSE/(n-k)).
It is not to be confused with the standard error of y itself (from descriptive statistics) or with the standard errors of the regression coefficients given below.

R² = 0.8025 means that 80.25% of the variation of y_i around ybar (its mean) is explained by the regressors x_2i and x_3i.
 

INTERPRET ANOVA TABLE

An ANOVA table is given. This is often skipped.
 

	df	SS	MS	F	Significance F
Regression	2	1.6050	0.8025	4.0635	0.1975
Residual	2	0.3950	0.1975
Total	4	2.0

The ANOVA (analysis of variance) table splits the sum of squares into its components.

Total sums of squares
= Residual (or error) sum of squares + Regression (or explained) sum of squares.

Thus Σ _i (y_i - ybar)² = Σ _i (y_i - yhat_i)² + Σ _i (yhat_i - ybar)²
where yhat_i is the value of y_i  predicted from the regression line
and ybar is the sample mean of  y.

For example:
R² = 1 - Residual SS / Total SS    (general formula for R²)
     = 1 - 0.3950 / 1.6050             (from data in the ANOVA table)
     = 0.8025                        (which equals R² given in the regression Statistics table).

The column labeled F gives the overall F-test of H0: β₂ = 0 and β₃ = 0 versus Ha: at least one of β₂ and β₃ does not equal zero.
Aside: Excel computes F this as:
F = [Regression SS/(k-1)] / [Residual SS/(n-k)] = [1.6050/2] / [.39498/2] = 4.0635.

The column labeled significance F has the associated P-value.
Since 0.1975 > 0.05, we do not reject H0 at signficance level 0.05.

Note: Significance F in general = FINV(F, k-1, n-k)  where k is the number of regressors including hte intercept.
Here  FINV(4.0635,2,2) = 0.1975.

INTERPRET REGRESSION COEFFICIENTS TABLE 

The regression output of most interest is the following table of coefficients and associated output:
 

	Coefficient	St. error	t Stat	P-value	Lower 95%	Upper 95%
Intercept	0.89655	0.76440	1.1729	0.3616	-2.3924	4.1855
HH SIZE	0.33647	0.42270	0.7960	0.5095	-1.4823	2.1552
CUBED HH SIZE	0.00209	0.01311	0.1594	0.8880	-0.0543	0.0585

Let β_j denote the population coefficient of the jth regressor (intercept, HH SIZE and CUBED HH SIZE).

Then

• Column "Coefficient" gives the least squares estimates of β_j.
• Column "Standard error" gives the standard errors (i.e.the estimated standard deviation) of the least squares estimates b_j of β_j.
• Column "t Stat" gives the computed t-statistic for H0: β_j = 0 against Ha: β_j ≠ 0.
  
This is the coefficient divided by the standard error. It is compared to a t with (n-k) degrees of freedom where here n = 5 and k = 3.
• Column "P-value" gives the p-value for test of H0: β_j = 0 against Ha: β_j ≠ 0..
  
This equals the Pr{|t| > t-Stat}where t is a t-distributed random variable with n-k degrees of freedom and t-Stat is the computed value of the t-statistic given in the previous column.
Note that this p-value is for a two-sided test. For a one-sided test divide this p-value by 2 (also checking the sign of the t-Stat).
• Columns "Lower 95%" and "Upper 95%" values define a 95% confidence interval for β_j.

     y = 0.8966 + 0.3365*x + 0.0021*z
 

CONFIDENCE INTERVALS FOR SLOPE COEFFICIENTS

95% confidence interval for slope coefficient β₂ is from Excel output (-1.4823, 2.1552).

Excel computes this as
   b₂ ± t_.025(3) × se(b₂)
= 0.33647 ± TINV(0.05, 2) × 0.42270
= 0.33647 ± 4.303 × 0.42270
= 0.33647 ± 1.8189
= (-1.4823, 2.1552).

TEST HYPOTHESIS OF ZERO SLOPE COEFFICIENT ("TEST OF STATISTICAL SIGNIFICANCE")

The coefficient of HH SIZE has estimated standard error of 0.4227, t-statistic of 0.7960 and p-value of 0.5095.
It is therefore statistically insignificant at significance level α = .05 as p > 0.05.

The coefficient of CUBED HH SIZE has estimated standard error of 0.0131, t-statistic of 0.1594 and p-value of 0.8880.
It is therefore statistically insignificant at significance level α = .05 as p > 0.05.

There are 5 observations and 3 regressors (intercept and x) so we use t(5-3)=t(2).
For example, for HH SIZE p = =TDIST(0.796,2,2) = 0.5095.
 

TEST HYPOTHESIS ON A REGRESSION PARAMETER

Here we test whether HH SIZE has coefficient β₂ = 1.0.

Example: H0: β₂ = 1.0 against Ha: β₂ ≠ 1.0 at significance level α = .05.

Then
  t = (b₂ - H0 value of β₂) / (standard error of b₂ )
    = (0.33647 - 1.0) / 0.42270
    = -1.569.

Using the p-value approach

• p-value = TDIST(1.569, 2, 2) = 0.257.  [Here n=5 and k=3 so n-k=2].
  
• Do not reject the null hypothesis at level .05 since the p-value is > 0.05.

• We computed  t = -1.569
• The critical value is t_.025(2) = TINV(0.05,2) = 4.303.  [Here n=5 and k=3 so n-k=2].
• So do not reject null hypothesis at level .05 since t = |-1.569| < 4.303.  

OVERALL TEST OF SIGNIFICANCE OF THE REGRESSION PARAMETERS

We test H0: β₂ = 0 and β₃ = 0 versus Ha: at least one of β₂ and β₃ does not equal zero.

From the ANOVA table the F-test statistic is 4.0635 with p-value of 0.1975.
Since the p-value is not less than 0.05 we do not reject the null hypothesis that the regression parameters are zero at significance level 0.05.
Conclude that the parameters are jointly statistically insignificant at significance level 0.05.

Note: Significance F in general = FINV(F, k-1, n-k)  where k is the number of regressors including hte intercept.
Here  FINV(4.0635,2,2) = 0.1975.
 

PREDICTED VALUE OF Y GIVEN REGRESSORS

Consider case where x = 4 in which case CUBED HH SIZE = x^3 = 4^3 = 64.

yhat  = b₁ + b₂ x₂ + b₃ x₃  =  0.88966 + 0.3365×4 + 0.0021×64 = 2.37006
 

EXCEL LIMITATIONS

Excel restricts the number of regressors (only up to 16 regressors ??).

Excel requires that all the regressor variables be in adjoining columns.
You may need to move columns to ensure this.
e.g. If the regressors are in columns B and D you need to copy at least one of columns B and D so that they are adjacent to each other.

Excel standard errors and t-statistics and p-values are based on the assumption that the error is independent with constant variance (homoskedastic).
Excel does not provide alternaties, such asheteroskedastic-robust or autocorrelation-robust standard errors and t-statistics and p-values.
More specialized software such as STATA, EVIEWS, SAS, LIMDEP, PC-TSP, ... is needed.

For further information on how to use Excel go to
     http://cameron.econ.ucdavis.edu/excel/excel.html